TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 5.4 De vergelijking x2 = c HAVO/VWO 2
Boek: Getal & Ruimte - Kwadraten en wortels HAVO/VWO 2 (deel 2) opgaven 47 t/m 59, 2013, 10e editie
47.
x2 = 49 heeft 2 oplossingen: x = 7 of x = -7
b.
x2 = 25 heeft 2 oplossingen: x = 5 of x = -5
c.
x2 = 0 heeft als oplossing: x = 0, dus 1 oplossing.
d.
x2 = -25 heeft geen oplossingen omdat een kwadraat nooit negatief kan zijn.
48.
b. Geen oplossingen, een kwadraat kan nooit negatief zijn.
c. x = √121 of x = -√121 levert x = 11 of x = -11
d. x = 0
e. x = √36 of x = -√36 levert x = 6 of x = -6
f. x = √1 of x = -√1 levert x = 1 of x = -1
g. x = √169 of x = -√169 levert x = 13 of x = -13
h. Geen oplossingen, een kwadraat kan nooit negatief zijn.
i. x = √0,09 of x = -√0,09 levert x = 0,3 of x = -0,3
49.
b. x = √25 of x = -√25 levert x = 5 of x = -5
c. x = √100 of x = -√100 levert x = 10 of x = -10
d. x = √9 of x = -√9 levert x = 3 of x = -3
e. Geen oplossingen, een kwadraat kan nooit negatief zijn.
f. x = √400 of x = -√400 levert x = 20 of x = -20
g. x = √15 of x = -√15 levert x ≈ 3,87 of x ≈ -3,87
h. x = 0
i. Geen oplossingen, een kwadraat kan nooit negatief zijn (-1/4).
50.
a. Bij t = 3,2 hoort h = 51,2 meter. Dus de hoogte van de toren is ongeveer 51 meter.
b. 5t2 = 112
c. t2 = 22,4 levert t ≈ 4,73 seconden
51.
r = 0,042 ⋅ (320)2 = 4300,8 meter
b.
0,042 ⋅ (v)2 = 2625
c.
0,042 ⋅ (v)2 = 2625
Links en rechts delen door :0,042
v2 = 62500
v = √62500 of v = -√62500
v = 250 of v = -250 (valt af!)
d.
0,042 ⋅ (v)2 = 3000
Links en rechts delen door :0,042
v2 = 71429
v = √71429 of v = -√71429
v ≈ 267,3 km/uur
52.
Los op: 0,1125x2 = 20
Links en rechts delen door: 0,1125
x2 = 177,78
x = √177,78 of x = -√177,78
x ≈ 13,33 of x ≈ -13,33
Het spandoek hangt tussen x = -13,33 en x = 13,33.
De breedte van het spandoek is dus: 2 x 13,33 = 26,66 meter.
Dat is 2666 cm.
b.
Los op: 0,1125x2 = 35
Links en rechts delen door: 0,1125
x2 = 311,11
x = √311,11 of x = -√311,11
x ≈ 17,64 of x ≈ -17,64
AB is dus: 2 x 17,64 = 35,28 meter.
Dat is 3528 cm.
53.
b. Geen oplossingen
c. x = 4 of x = -4
d. x = 5 of x = -5
e. x = 3 of x = -3
f. x = 9 of x = -9
54.
a. x = 0
b. x = 1 of x = -1
c. x = 5 of x = -5
d. x = 0
e. x = 5 of x = -5
f. x = 6 of x = -6
g. x = 10 of x = -10
h. x = 4 of x = -4
i. Geen oplossingen
55.
2x2 = 8
x2 = 4
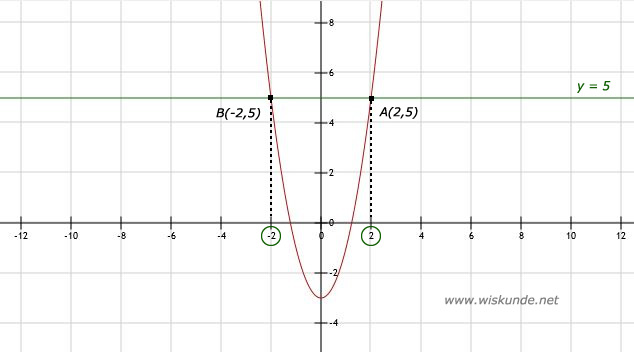
x = √4 of x = -√4
x = 2 of x = -2 (dit zijn de x-coördinaten van de snijpunten op de x-as.)
x = 2 invullen, levert: y = 2⋅(2)2 - 3 = 8 - 3 = 5. Dus punt A(2,5).
x = -2 invullen, levert: y = 2⋅(-2)2 - 3 = 8 - 3 = 5. Dus punt B(-2,5).
56.
1/4x2 = 9
Nu links en rechts keer 4
x2 = 36
x = √36 of x = -√36
x = 6 of x = -6
Snijpunten: D(-6,5) en E(6,5).
b. Los op: -2x2 + 5 = -13
-2x2 = -18
x2 = 9
x = √9 of x = -√9
x = 3 of x = -3
Snijpunten: P(-3,-13) en Q(3,-13).
Tip:
De vergelijking x2 = c kan 2, 1 of geen oplossingen hebben.
a. De vergelijking x2 = c kan 2, 1 of geen oplossingen hebben.
x2 = 49 heeft 2 oplossingen: x = 7 of x = -7
b.
x2 = 25 heeft 2 oplossingen: x = 5 of x = -5
c.
x2 = 0 heeft als oplossing: x = 0, dus 1 oplossing.
d.
x2 = -25 heeft geen oplossingen omdat een kwadraat nooit negatief kan zijn.
48.
Tip:
Bij x2 = c:
c > 0 dan 2 oplossingen
c = 0 dan 1 oplossing
c < 0 dan geen oplossingen
a. x = √13 of x = -√13 levert x ≈ 3,61 of x ≈ -3,61Bij x2 = c:
c > 0 dan 2 oplossingen
c = 0 dan 1 oplossing
c < 0 dan geen oplossingen
b. Geen oplossingen, een kwadraat kan nooit negatief zijn.
c. x = √121 of x = -√121 levert x = 11 of x = -11
d. x = 0
e. x = √36 of x = -√36 levert x = 6 of x = -6
f. x = √1 of x = -√1 levert x = 1 of x = -1
g. x = √169 of x = -√169 levert x = 13 of x = -13
h. Geen oplossingen, een kwadraat kan nooit negatief zijn.
i. x = √0,09 of x = -√0,09 levert x = 0,3 of x = -0,3
49.
Tip:
x2 = 16, dwz: bereken de x-coördinaten van de snijpunten van de parabool (x2) met de horizontale lijn y = 16. Maak maar eens een schets!
a. x = √11 of x = -√11 levert x ≈ 3,32 of x ≈ -3,32x2 = 16, dwz: bereken de x-coördinaten van de snijpunten van de parabool (x2) met de horizontale lijn y = 16. Maak maar eens een schets!
b. x = √25 of x = -√25 levert x = 5 of x = -5
c. x = √100 of x = -√100 levert x = 10 of x = -10
d. x = √9 of x = -√9 levert x = 3 of x = -3
e. Geen oplossingen, een kwadraat kan nooit negatief zijn.
f. x = √400 of x = -√400 levert x = 20 of x = -20
g. x = √15 of x = -√15 levert x ≈ 3,87 of x ≈ -3,87
h. x = 0
i. Geen oplossingen, een kwadraat kan nooit negatief zijn (-1/4).
50.
a. Bij t = 3,2 hoort h = 51,2 meter. Dus de hoogte van de toren is ongeveer 51 meter.
b. 5t2 = 112
c. t2 = 22,4 levert t ≈ 4,73 seconden
51.
Tip:
De negatieve wortel is niet altijd zinvol. Je kunt bijv. geen negatieve afstanden of snelheden hebben.
a.De negatieve wortel is niet altijd zinvol. Je kunt bijv. geen negatieve afstanden of snelheden hebben.
r = 0,042 ⋅ (320)2 = 4300,8 meter
b.
0,042 ⋅ (v)2 = 2625
c.
0,042 ⋅ (v)2 = 2625
Links en rechts delen door :0,042
v2 = 62500
v = √62500 of v = -√62500
v = 250 of v = -250 (valt af!)
d.
0,042 ⋅ (v)2 = 3000
Links en rechts delen door :0,042
v2 = 71429
v = √71429 of v = -√71429
v ≈ 267,3 km/uur
52.
Tip:
Bekijk goed de x-as en de h-as in de afbeelding.
AB is lijnsymmetrisch ten opzichte van de verticale h-as.
a.Bekijk goed de x-as en de h-as in de afbeelding.
AB is lijnsymmetrisch ten opzichte van de verticale h-as.
Los op: 0,1125x2 = 20
Links en rechts delen door: 0,1125
x2 = 177,78
x = √177,78 of x = -√177,78
x ≈ 13,33 of x ≈ -13,33
Het spandoek hangt tussen x = -13,33 en x = 13,33.
De breedte van het spandoek is dus: 2 x 13,33 = 26,66 meter.
Dat is 2666 cm.
b.
Los op: 0,1125x2 = 35
Links en rechts delen door: 0,1125
x2 = 311,11
x = √311,11 of x = -√311,11
x ≈ 17,64 of x ≈ -17,64
AB is dus: 2 x 17,64 = 35,28 meter.
Dat is 3528 cm.
53.
Tip:
Zorg ervoor dat x2 links staat en de gewone getallen rechts.
Deel als laatste stap links en rechts door het getal dat voor de x2 staat (balansmethode).
a. x = 1 of x = -1 Zorg ervoor dat x2 links staat en de gewone getallen rechts.
Deel als laatste stap links en rechts door het getal dat voor de x2 staat (balansmethode).
b. Geen oplossingen
c. x = 4 of x = -4
d. x = 5 of x = -5
e. x = 3 of x = -3
f. x = 9 of x = -9
54.
a. x = 0
b. x = 1 of x = -1
c. x = 5 of x = -5
d. x = 0
e. x = 5 of x = -5
f. x = 6 of x = -6
g. x = 10 of x = -10
h. x = 4 of x = -4
i. Geen oplossingen
55.
Tip:
Bereken de snijpunten van een parabool met een horizontale lijn.
Los op: 2x2 - 3 = 5Bereken de snijpunten van een parabool met een horizontale lijn.
2x2 = 8
x2 = 4
x = √4 of x = -√4
x = 2 of x = -2 (dit zijn de x-coördinaten van de snijpunten op de x-as.)
x = 2 invullen, levert: y = 2⋅(2)2 - 3 = 8 - 3 = 5. Dus punt A(2,5).
x = -2 invullen, levert: y = 2⋅(-2)2 - 3 = 8 - 3 = 5. Dus punt B(-2,5).

56.
Tip:
Bereken de snijpunten van een parabool met een horizontale lijn.
a. Los op:
1/4x2 - 4 = 5Bereken de snijpunten van een parabool met een horizontale lijn.
1/4x2 = 9
Nu links en rechts keer 4
x2 = 36
x = √36 of x = -√36
x = 6 of x = -6
Snijpunten: D(-6,5) en E(6,5).
b. Los op: -2x2 + 5 = -13
-2x2 = -18
x2 = 9
x = √9 of x = -√9
x = 3 of x = -3
Snijpunten: P(-3,-13) en Q(3,-13).
57.
8 = a⋅(125)2
15625a = 8
a = 8/15625
a = 0,000512
58.
x2 = 50
x = √50 of x = -√50
√50 = √25 x √2 = 5√2
x = 5√2 of x = -5√2
b.
x2 = 5 4/9
x2 = 49/9
x = √(49/9) of x = -√(49/9)
x = √49/√9 of x = -√49/√9
x = 7/3 of x = -7/3
x = 2 1/3 of x = -2 1/3
c.
x2 = 200
x = √200 of x = -√200
√200 = √100 x √2 = 10√2
x = 10√2 of x = -10√2
d.
1/5x2 + 10 = 60
1/5x2 = 50
Nu links en rechts: keer 5 (breuken wegwerken)
x2 = 250
x = √250 of x = -√250
√250 = √25 x √10 = 5√10
x = 5√10 of x = -5√10
e.
2x2 - 6 = 74
2x2 = 80
x2 = 40
x = √40 of x = -√40
√40 = √4 x √10 = 2√10
x = 2√10 of x = -2√10
f.
-x2 + 1/2 = -1 3/4
-x2 = -2 1/4
Links en rechts: keer -1
x2 = 2 1/4
x2 = 9/4
x = √(9/4) of x = -√(9/4)
x = 3/2 of x = -3/2
x = 1,5 of x = -1,5
59.
x2 + 5 = 85
Links en rechts: -5
x2 = 80
x = √80 of x = -√80
√80 = √16 x √5 = 4√5
x = 4√5 of x = -4√5
b.
1/4x2 - 3 = 5
Links en rechts: +3
1/4x2 = 8
Links en rechts: x4 (breuken wegwerken)
x2 = 32
x = √32 of x = -√32
√32 = √16 x √2 = 4√2
x = 4√2 of x = -4√2
c.
25x2 - x2 = 6
24x2 = 6
Links en rechts: :24
x2 = 6/24 = 1/4
x = √1/4 of x = -√1/4
x = 1/2 of x = -1/2
d.
16x2 - 1 = 0
Links en rechts: +1
16x2 = 1
Links en rechts: deel door 16
x2 = 1/16
x = √(1/16) of x = -√(1/16)
x = √1/√16 of x = -√1/√16
x = 1/4 of x = -1/4
e.
5x2 - 54 = 2x2
Links en rechts: -2x2
3x2 - 54 = 0
Links en rechts: +54
3x2 = 54
Links en rechts: deel door 3
x2 = 18
x = √18 of x = -√18
√18 = √9 x √2 = 3√2
x = 3√2 of x = -3√2
f.
x2 + 24 = 2x2
Links en rechts: -2x2
-x2 + 24 = 0
Links en rechts: -24
-x2 = -24
Links en rechts: deel door -1
x2 = 24
x = √24 of x = -√24
√24 = √4 x √6 = 2√6
x = 2√6 of x = -2√6
Tip:
We weten 2 punten die op de parabool liggen: (-125,8) en (125,8).
Vul het punt (125,8) in y = ax2We weten 2 punten die op de parabool liggen: (-125,8) en (125,8).
8 = a⋅(125)2
15625a = 8
a = 8/15625
a = 0,000512
58.
Tip:
√a / √b = √(a/b)
√a x √b = √(ab)
a. √a / √b = √(a/b)
√a x √b = √(ab)
x2 = 50
x = √50 of x = -√50
√50 = √25 x √2 = 5√2
x = 5√2 of x = -5√2
b.
x2 = 5 4/9
x2 = 49/9
x = √(49/9) of x = -√(49/9)
x = √49/√9 of x = -√49/√9
x = 7/3 of x = -7/3
x = 2 1/3 of x = -2 1/3
c.
x2 = 200
x = √200 of x = -√200
√200 = √100 x √2 = 10√2
x = 10√2 of x = -10√2
d.
1/5x2 + 10 = 60
1/5x2 = 50
Nu links en rechts: keer 5 (breuken wegwerken)
x2 = 250
x = √250 of x = -√250
√250 = √25 x √10 = 5√10
x = 5√10 of x = -5√10
e.
2x2 - 6 = 74
2x2 = 80
x2 = 40
x = √40 of x = -√40
√40 = √4 x √10 = 2√10
x = 2√10 of x = -2√10
f.
-x2 + 1/2 = -1 3/4
-x2 = -2 1/4
Links en rechts: keer -1
x2 = 2 1/4
x2 = 9/4
x = √(9/4) of x = -√(9/4)
x = 3/2 of x = -3/2
x = 1,5 of x = -1,5
59.
Tip:
Probeer je antwoord eens te controleren of het klopt!
a. Probeer je antwoord eens te controleren of het klopt!
x2 + 5 = 85
Links en rechts: -5
x2 = 80
x = √80 of x = -√80
√80 = √16 x √5 = 4√5
x = 4√5 of x = -4√5
b.
1/4x2 - 3 = 5
Links en rechts: +3
1/4x2 = 8
Links en rechts: x4 (breuken wegwerken)
x2 = 32
x = √32 of x = -√32
√32 = √16 x √2 = 4√2
x = 4√2 of x = -4√2
c.
25x2 - x2 = 6
24x2 = 6
Links en rechts: :24
x2 = 6/24 = 1/4
x = √1/4 of x = -√1/4
x = 1/2 of x = -1/2
d.
16x2 - 1 = 0
Links en rechts: +1
16x2 = 1
Links en rechts: deel door 16
x2 = 1/16
x = √(1/16) of x = -√(1/16)
x = √1/√16 of x = -√1/√16
x = 1/4 of x = -1/4
e.
5x2 - 54 = 2x2
Links en rechts: -2x2
3x2 - 54 = 0
Links en rechts: +54
3x2 = 54
Links en rechts: deel door 3
x2 = 18
x = √18 of x = -√18
√18 = √9 x √2 = 3√2
x = 3√2 of x = -3√2
f.
x2 + 24 = 2x2
Links en rechts: -2x2
-x2 + 24 = 0
Links en rechts: -24
-x2 = -24
Links en rechts: deel door -1
x2 = 24
x = √24 of x = -√24
√24 = √4 x √6 = 2√6
x = 2√6 of x = -2√6
Andere paragrafen:
5.1. Kwadratische formules (1 t/m 11)
5.2. Wortelformules (12 t/m 20)
5.3. Rekenen met wortels (21 t/m 46)
5.4. De vergelijking x2 = c (47 t/m 59)
5.5. Soorten getallen (60 t/m 73)
5.1. Kwadratische formules (1 t/m 11)
5.2. Wortelformules (12 t/m 20)
5.3. Rekenen met wortels (21 t/m 46)
5.4. De vergelijking x2 = c (47 t/m 59)
5.5. Soorten getallen (60 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


